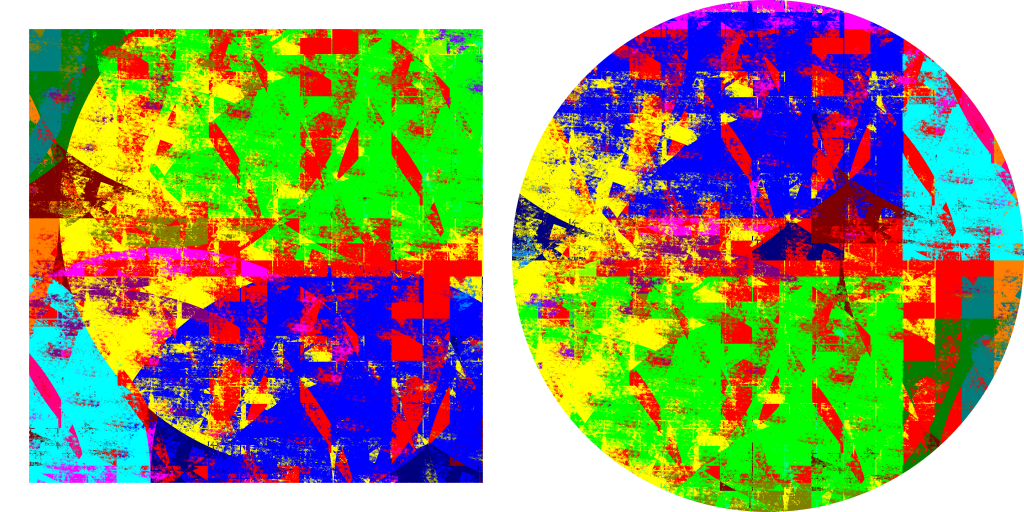
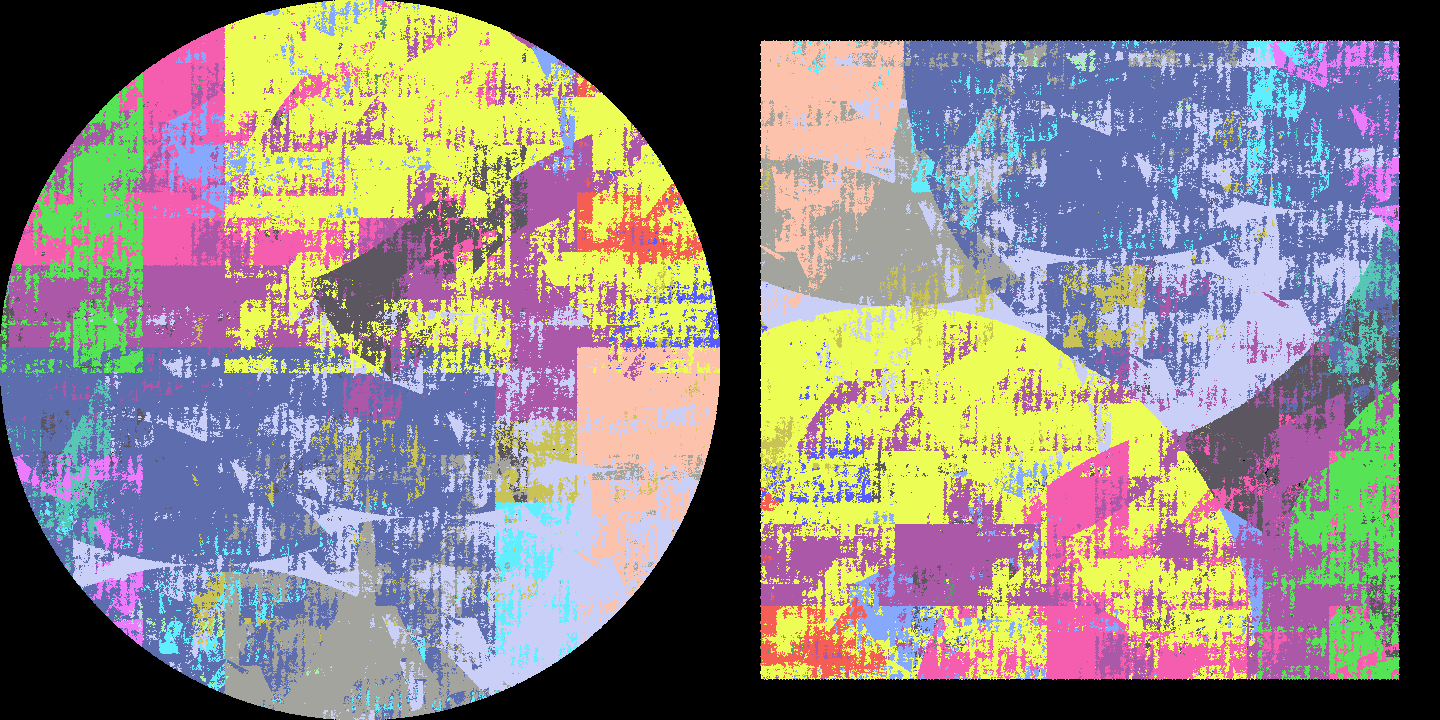
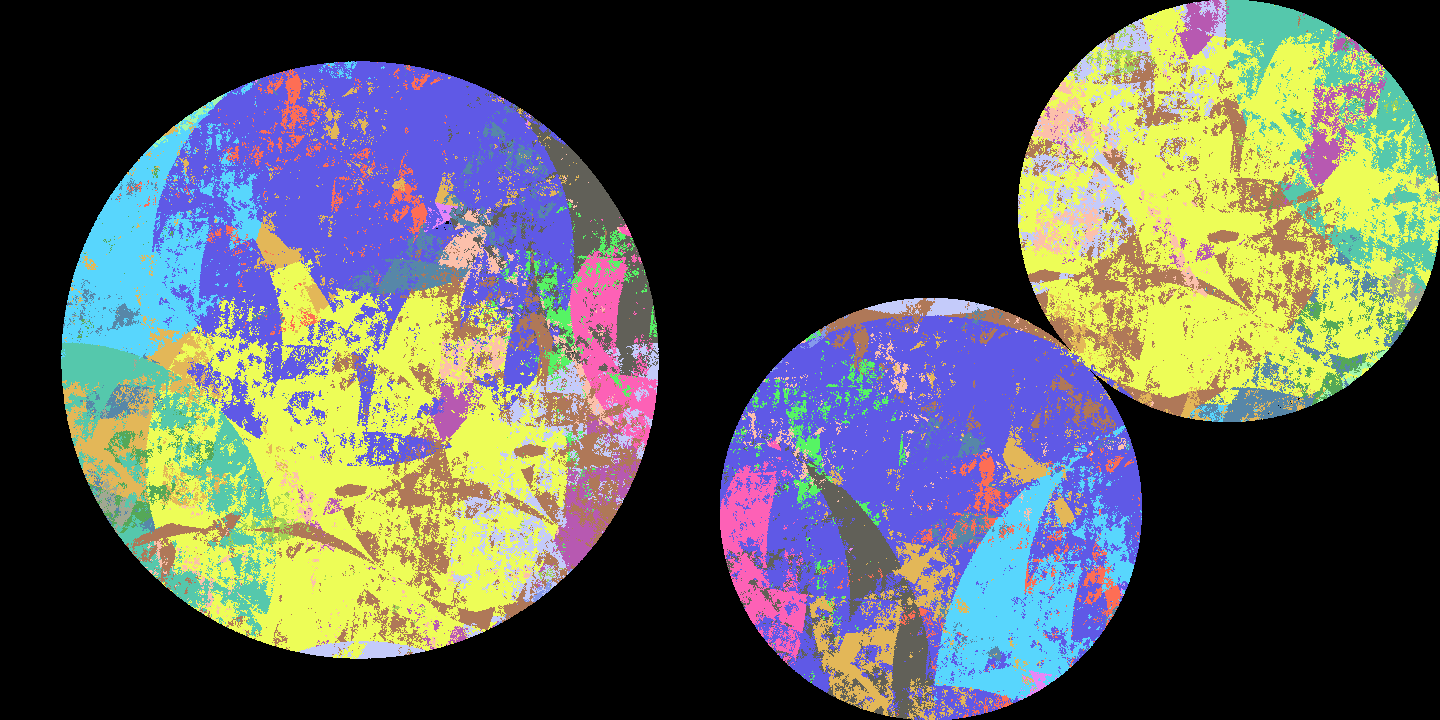大家好我是渡鸦,今天和大家聊一聊下面这张图片的来龙去脉。(图片来源[1],点开图片看大图)
早在中国明清时期,一种现在广为人知的拼图玩具——七巧板,就已经沿宋朝的“燕几图”为雏形,发展成熟成了今天的样子。无独有偶,几何盛行的古希腊时期,阿基米德也发明了名为Ostomachion的拼图玩具(见下图,图源维基百科),玩法与中国的七巧板无异。

在人们惊叹于七巧板类玩具变化的多种多样的同时,另一类和七巧板略有不同的拼图谜题也从几何学家的写写画画之中悄然诞生了。与七巧板“给定数个固定的拼图板块,尝试拼出某些新的形状”的挑战正相反,这种新的拼图谜题的宗旨是“给定几个固定的图形,构造数个拼图组件的形状,使得用这些组件能够一一拼出这些给定的图形”。而这,就是今天的主题——“等拆分谜题”(dissection puzzle)。
翻开Greg Frederickson的书[2],就能轻易了解到等拆分谜题的简史。1774年清乾隆三十九年,学者戴震为四库全书馆修订当时只剩下残抄本的《九章算术》[3],其中对于刘辉关于正十二边形面积的计算,他凭自己的理解补充了类似下面的一张图:
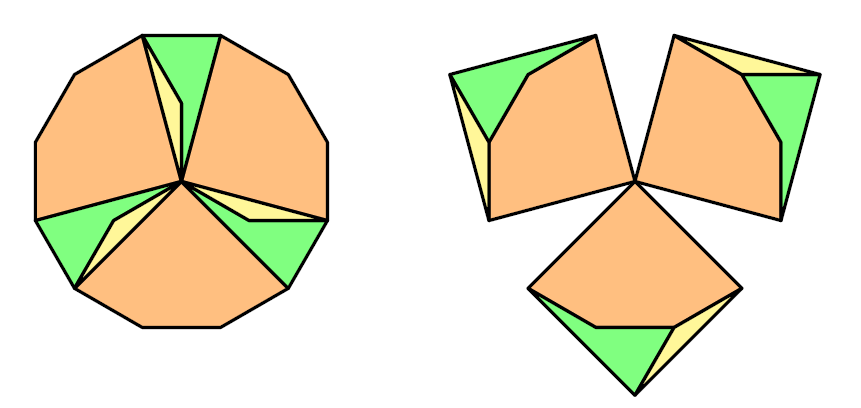
图中左面将一个正十二边形拆分成九个部分,而只通过把各个部分简单地平移,就能得到右边的三个正方形,这就是现存最早的等拆分谜题之中很知名的一个了。在西方,等拆分谜题也在同一个世纪逐步盛行,到十九世纪则出现了大批的可考资料。到二十世纪初,这类谜题受到谜题大师Sam Loyd(美)和Henry Dudeney(英)等人的青睐,更是占据了数个英美报纸杂志的解谜板块。在这样的影响下,就出现了下面这张后来最广为人知的“正方形变三角形四块”(Dudeney 1902,图源维基百科)。

对于更一般的两个多边形,早在前一个世纪初就有Wallace、Lowry、Bolyai、Gerwien各自独立发现的定理:
| 多边形等拆分定理(Wallace 1807、Lowry 1814?、Bolyai 1833、Gerwien 1835):
给定两个面积相等的平面多边形,可以把其中一个拆分成有限若干块小多边形,通过平移、旋转、重新组合得到另一个给定的多边形。 |
关于这个定理的简单证明可以参考互动网站[4](仅PC端可用,手机请百度搜索其他非互动证明),更多多边形等拆分的例子可以参考B站帆雨动画制作的视频系列[5],其他相关内容这里暂不赘述。
随着越来越多人加入探索等拆分谜题可能性的热潮,谜题的不同花样也越来越多。1901年Sam Loyd给出了下面这个“3²+4²=5²”的谜题,这里不仅和戴震的构造一样设置了“只能平移板块、不能对称旋转”的要求,还限制了每个板块必须是贴合网格线的形状:
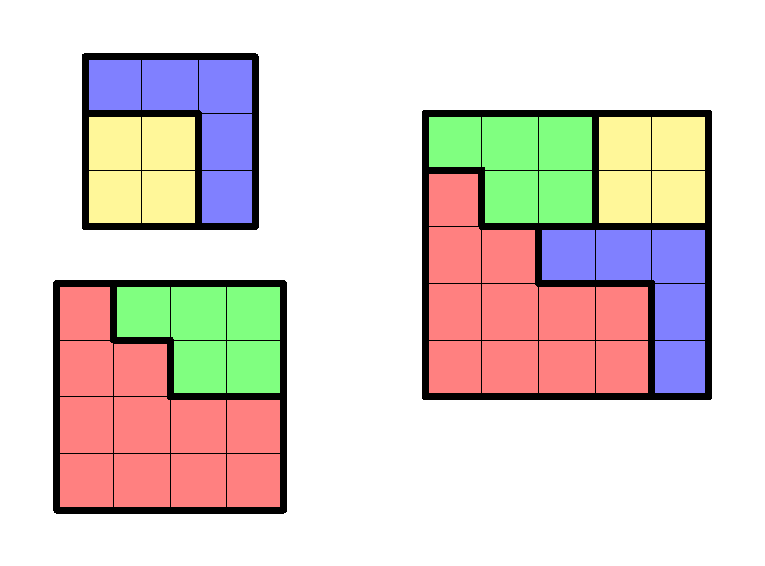
1900年,德国著名数学家大卫·希尔伯特(David Hilbert)在法国巴黎的国际数学家大会上,面向二十世纪全球的数学家们提出了著名的二十三个问题,其中包括连续统假设、黎曼猜想之类的二十世纪数学领域中的大明星,而其第三个问题的叙述是这样的:“给定两个等体积的多面体,能否将其中一个分割成有限若干块小多面体,继而重新组合形成其中另一个?”这是在问等拆分定理是否也在三维空间中成立。
不到一年,希尔伯特的学生马克斯·德恩(Max Dehn)在1901年给出了第三问题的否定回答,随之该问题就成为了二十三个问题中最早被拿下的一个。给定一个空间多面体,德恩构思出了一个基于各个二面角组合而出的张量,史称“德恩不变量”(Dehn invariant)。德恩和后来的Jean-Pierre Sydler (1965)共同发现,对于任意两个空间多面体,可以把其中一个多面体由有限个小多面体组件拆分再重组成另一个的充分必要条件就是,两者的体积和德恩不变量两个数值都对等。同时,由计算得出的是一个正方体的德恩不变量和相等体积的正四面体的德恩不变量并不相等,因此这一对多面体就成为了希尔伯特第三问题的一个反例。三维内的可等拆分性问题被解决了,但我们同时也注意到了更高维度给等拆分问题带来的更大限制,看似在三维空间中构造等拆分就变得比二维更不自由了。
二十年后,在1924年,波兰数学家斯特凡·巴拿赫(Stefan Banach)和美国籍波兰裔数学家阿尔弗雷德·塔斯基(Alfred Tarski)基于德国数学家豪斯多夫(Felix Hausdorff)的成果联合发表的一篇论文如晴天霹雳,其余波将震撼数学的大厦数十年。他们发现的就是:
| 巴拿赫-塔斯基分球悖论(1924,后由Raphael Robinson 1947 [8]最优化):
可以把一个单位体积的球体拆分成五个集合,再把它们各自平移、旋转、重新组合,得到两个一样的单位体积的球。 更一般地,给定三维空间内任意两个有体积的简单几何体,都可以把其中一个拆分成有限若干个集合,通过平移、旋转、重新组合,得到另一个。 |
当然,在这样的拆分过程中,每个部分组件都不再是简单的三维几何体,而是必须用集合论的语言才能准确描绘的复杂形状。这个悖论的具体证明和相关讨论参见Vsauce的视频[6],下面是张视频里的截图:

关于巴拿赫-塔斯基分球悖论的史话,我是从Grzegorz Tomkowicz和Stan Wagon的书[7]中学到的。
巴拿赫-塔斯基分球悖论,用更准确的语言说是这么一回事:如果要想在三维空间里定义“体积”的概念,那就不能同时满足这三个要求:
-
-
- 普适性:每个有限大的形状都能测出体积;
- 可加性:给定有限若干个两两互不重叠的集合,它们总共的体积等于它们各自体积的总和;
- 不变性:把一个集合任意平移或旋转,变换前后之间体积不发生改变。
-
如果想同时满足这三点要求,那么由分球悖论的存在,就没法避免得出球体体积1=2的矛盾。
这里不得不提到,和其他某些悖论一样,当人们注意到这三点之间存在相互矛盾的时候,总有更富有创造力的人能琢磨出这个矛盾的别的体现方式。取一个单位球体,去掉其中心的一个点,称它为“单位去心球”。在1947年Raphael Robinson于其论文[8]证明了,存在这样一个空间集合:取三个一模一样的这个集合,通过各自绕球心进行三维旋转,可以组合成这样一个单位去心球。但如果取四个一模一样的这个集合,重新各自绕球心进行三维旋转,也可以组合成同一个单位去心球。也就是说,这个集合要是有体积,那么它既能等于单位球体积的三分之一,也能等于单位球体积的四分之一。
说回分球悖论。既然“体积”的定义不能同时满足前面列出的三点,那么只要去掉任意一点,剩余两点也可以凑活着用。这样的“舍一保二”对“体积”的概念有什么影响呢?如果去掉第一点普适性,就相当于把目光只局限在可以简单定义体积的经典几何体上面,我们这就重新回到了熟悉的古典几何学上。如果去掉第二点可加性,那么“体积”的概念就完全不再实用,不纳入考虑范围内。第三点的不变性是不是也不该舍弃呢?巧就巧在,要是只去掉这第三点不变性的一半,不仅原有的矛盾消失了,还有一条连接几何学和群论的崭新纽带展现在当时的人们眼前。
要聊这事,就得重新审视分球悖论的证明了。不管具体如何,分球悖论的每一种已知证明似乎都不谋而合地提到了同一件事:球面上的点,可以至少绕两条独立的旋转轴分别旋转。乍一看这挺像一句废话,但在分球悖论后十年内,巴拿赫和冯·诺依曼联合发现的结果恰恰说明了它对于整个分球悖论是不可或缺的。他们提出:
| 不变扩张定理(巴拿赫 1923、冯·诺依曼 1929):
固定三维空间内最多一条旋转轴的朝向,那么存在一种“体积”的定义,其满足之前的第一点普适性、第二点可加性,还有稍微弱一些的不变性:把一个集合平移,或是沿着这个固定的旋转轴朝向做旋转,变换前后的集合体积不变。 类似的结论在其他维度和空间中也成立。 |
因此若是在分球悖论的证明里,只允许球面上的点要么全朝同一个方向旋转要么不旋转,那么由于这种自洽的体积的存在,就不论如何也导不出体积1=2的矛盾了。
有了这些准备,我们终于可以回到二维的平面世界上来,解答这样一个问题:二维的圆形、乃至任意多边形,会不会也受到“分圆悖论”的影响呢?可以发现,在二维的平面上不论怎么旋转,都是在沿同一个朝向——即以垂直平面的方向为旋转轴。因此不变扩张定理适用:假设我们可以把某个平面图形拆分成数块,再依次平移、旋转、重新组合,得到另外某个平面图形,那就可以再接着用不变扩张定理赋予的新的“二维面积”衡量拼图的每一小块。由于这种面积同时满足普适性、可加性和囊括了所有二维旋转方向的不变性,我们必然能推断出拆分之前的图形和拼组出的新图形,两者的二维面积是相等的!这么一个自洽的“二维面积”就史称“巴拿赫测度”,以纪念巴拿赫做出的贡献。
这时候有人就会问了,既然我们已经知道“两个可等拆分的平面图形,其面积一定相等”,那么反之是不是也成立呢?问这个的还不是别人,正是分球悖论的另一发现者阿尔弗雷德·塔斯基。他在分球悖论问世的转年1925年向数学界发问:
| 塔斯基的化圆为方问题(1925):
一个单位面积的圆,可不可以拆分成有限的数个小块,再通过平移、旋转、重新组合,形成一个同是单位面积的正方形? |
他对别的几何图形一概不问,而只取圆和方这两个特殊例子的原因有二:其一,“化圆为方”这个名字不是首次出现,古希腊时期同名的著名无解问题问的就是能否凭尺规作图构造出一对面积一样的圆和方,今日塔斯基再问,形成一个数学史的前后照应;其二,要是一如既往地沿用简单几何形状来拼组,那么圆形的弧线再怎么剪接都不能完全转化成正方形的直边,欲化圆为方,须另辟蹊径。
问题提出之后,六十五年无人能答。虽然很多人跃跃欲试,但最后都功败垂成。二十世纪末1990年,匈牙利数学家米克洛什·拉兹科维奇(Miklós Laczkovich)一鸣惊人,运用了横跨数论、傅里叶分析、图论和测度论等多个领域的绝技,实现了一种各个组件只平移不旋转的等拆分,给化圆为方问题提交了充分肯定的解答。后于1992年,又提交了一份更简练的证明,一并证实了任意维度中不靠组件旋转而“化球为立方”的可行性。接下来讲的就是他1992年的证明思路。
| 可等拆分性定理(拉兹科维奇 1992 [9]):
取两个足够简单的二维几何图形,例如圆和方。若两者面积相等,则可把其中一个拆分成有限若干个集合,再通过各自平移和重新组合,形成另一个。 类似的结论在其他维度中也成立。 |
注意:为了展示核心思想,以下对原证明做了大幅简化,想参考严谨证明或了解特定细节的读者请查阅原版文献[9]。
我们从一个特殊的构造着手。
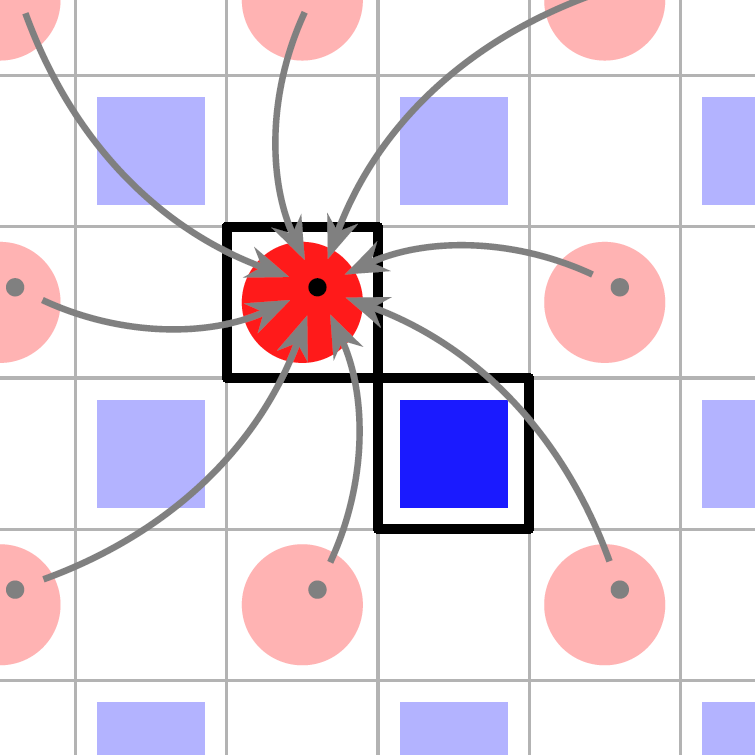
如图所示,把给定的圆形和方形放到一个正方形网格内,再周期性地充满整个平面。这些复制品不会独立存在,而都会和初始的图形保持对应。比如,我们要是在之后规定某个圆形上的某点属于某一个拆分组件,那么原始圆形上对应位置的点连带着所有圆形上同样位置的点都会同属于这个组件。
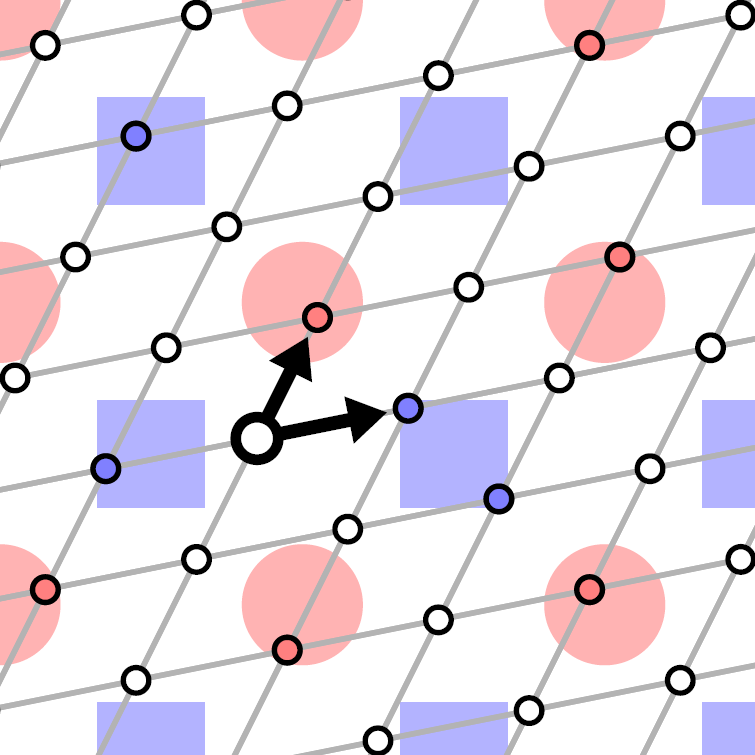
再如上图,挑任意一个平面点作为起点,任选一个网格朝向,构建一个格点网络。在每个格点上采样,记录其是否落在圆和方的区域内,形成一个采样网格。拉兹科维奇发现,这样的采样结果有办法精准地近似整个平面:
| 密度估计引理:
有一种近乎随机的网格朝向,使得不管从哪个起始点开始沿这个朝向的网格采样,圆和方的图形区域在采样格点网上的分布都尽可能均匀,且均匀分布的密度大小都等于该图形区域占整个平面的密度,即和图形本身的面积成正比。 |
可以想象从平面上的每个点开始,都沿同一固定朝向构建一个采样网格,看起来会像是一个网格的许多平移版本。不同网格上的采样点不会互相重叠,而平面上的每个点都隶属于其中某一个网格之内。我们将对每个采样网格单独处理,这就既能同时处理平面上的所有点,又不会在处理不同的采样网格时相互干扰。
取其中一个采样网格。我们想要其中每个属于圆形的格点都在其所属组件移动后变成一个属于方形的格点,例如下图所示。

又由之前的密度估计引理,这些圆形格点和方形格点在格网上是一比一混匀的。要想给这些点一一配成对,那好像只要给每个点都就近配对就够了。这一步所需的关键,是图论中判断一一配对存在性的标准流程,我们用一个术语尽量少的比方来描述:
| 霍尔婚配定理(Philip Hall 1935、Rado 1967、Marshall Hall 1986):
假设若干顾客来一家有若干商品的超市购物,每位顾客都有其看得上的数件商品。再假设任意有限位顾客看上的商品数不比他们人数少(即不会不够分),任意有限件商品能被看上的人数也不比这个商品数少(即不会买不完),那么有一种一一分配的方式,使每位顾客能买到恰好一件看得上的商品,每件商品能恰好被一位能看得上的顾客买走。 |
在采样网格里,我们就把属于圆的格点比作是顾客,把属于方的格点比作是商品。事先确定一个足够大的半径,让每位顾客都能看得上其周围这个半径范围内的所有商品,从而能看得上某一件商品的就是其周围这个半径范围内的顾客们。由于顾客和商品两方在格点网上是一比一混合均匀的,任意一方中任取有限多个都会被至少同等多的另一方所包围,因而霍尔婚配定理适用。我们可知,每个采样网格上都存在一种圆区域格点和方区域格点的一一配对方式,且每一对格点间的距离都不超过一个确定的半径。
我们把每个圆形格点都移动到与之配对的方形格点上,形成一种从圆到方的打乱重组。由于和每个圆形点配对的,都一定是在同一网格内的固定半径范围内的格点,所以每个点移动的方向和距离都只有固定的有限多种可能性,如下图所示。
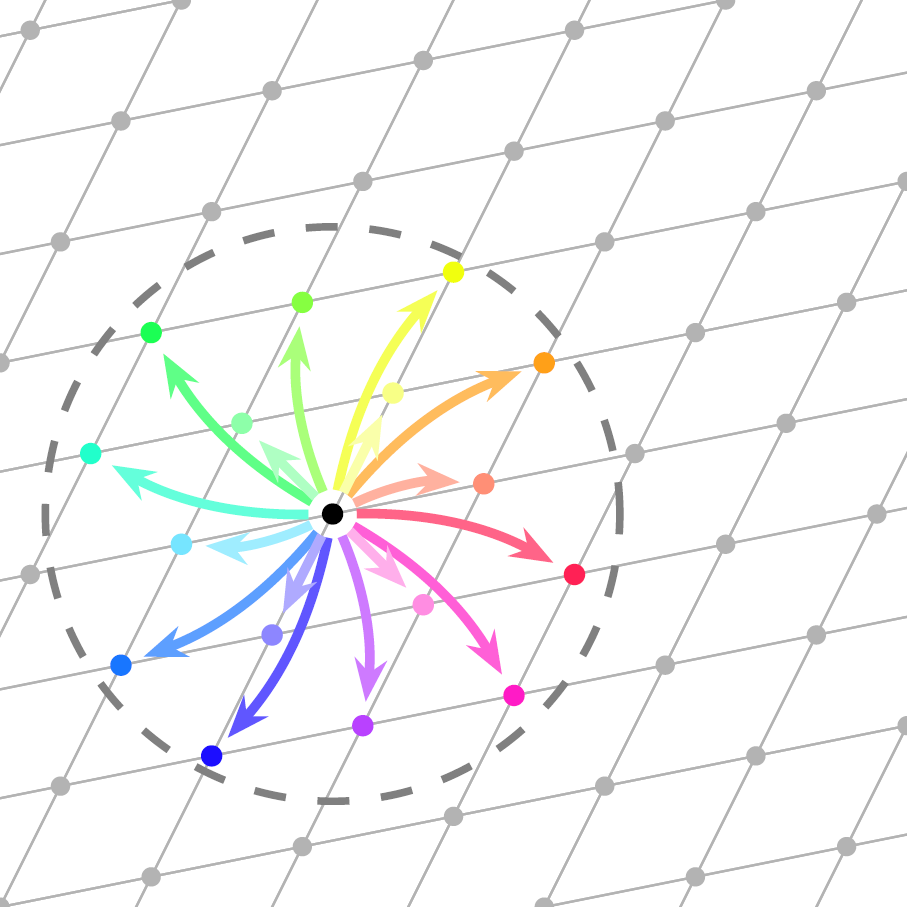
如果把初始给定的圆形内的所有点按照其移动方向和距离归类,就可以把圆形分成有限多个部分,且每个部分中的所有点都是沿相同方式平移的。而这,就是只靠平移而化圆为方的等拆分方法了。QED
关键的定理证明完了,就再聊一点史话。拉兹科维奇的等拆分虽然给出了可行性,但是其效率还不够令人满意。这个构造之中的各个拆分组件要是不用上不变扩张定理就根本测不出面积,而这样的拆分组件又总共用了约10的40次方个。究其原因,能影响到组件的几何复杂度的主要就是霍尔婚配定理,而关系到组件个数的则是密度估计引理中的误差项。
以拉兹科维奇的采样网格构造为基准,又以提高两个关键引理的效率为目标,拉兹科维奇和更后来的Grabowski–Máthé–Pikhurko (2015 [10])、Marks–Unger (2016 [11])、Bowen–Kun–Sabok (2021 [12])、Máthé–Noel–Pikhurko (2022 [13])依次提升了化圆为方等拆分的效率。本期文章开头的图片,就是论文[11]的作者之一Andrew Marks对其构造的渲染,其中每个拆分组件用标准的数学分析就可测得面积,而整个等拆分只用到了22个组件。
笔者有幸联系到了标题图的作者Andrew Marks,然后用他的算法渲染了以下的图片:
一:图中是经典的化圆为方。
二:图中是只由平移完成的一个正三角形的半周旋转。这个特殊的等拆分的存在性是拉兹科维奇于1990年证明化圆为方(见[7]的第九章)所用到的一条引理,当然只用多边形拼图组件纯靠平移是拼不出来的。
三:图中是把一个圆均分成两个圆的过程,以致敬巴拿赫-塔斯基分球悖论的近一百年历史。
和往常一样,感谢您的阅读。
参考文献和扩展阅读:
-
- 标题图:Andrew Marks, Pictures of Borel Circle Squaring
- 等拆分谜题的介绍:Greg N. Frederickson, Dissections: Plane and Fancy
- 《九章算术》,版本与校勘
- 多边形等拆分定理的证明(仅PC端可用,手机请百度搜索其他证明):Dima Smirnov & Zivvy Epstein, Scissors Congruence
- 多边形等拆分的视频系列:帆雨动画,几何裁切
- 巴拿赫-塔斯基分球悖论的视频:Vsauce,分球悖论:一个球变两个球(巴拿赫-塔斯基悖论),昨梦电羊译
- 巴拿赫-塔斯基分球悖论的书籍(第九章有拉兹科维奇1990年的证明介绍):Grzegorz Tomkowicz & Stan Wagon, The Banach–Tarski Paradox
- 分球悖论相关论文:Raphael Robinson, On the decomposition of spheres
- 化圆为方论文:Miklós Laczkovich, Decomposition of sets with small boundary
- 化圆为方相关论文:Łukasz Grabowski & András Máthé & Oleg Pikhurko, Measurable circle squaring
- 化圆为方相关论文:Andrew Marks & Spencer Unger, Borel Circle Squaring
- 化圆为方相关论文:Matthew Bowen & Gabor Kun & Marcin Sabok, Perfect matchings in hyperfinite graphings
- 化圆为方相关论文:András Máthé & Jonathan A. Noel & Oleg Pikhurko, Circle Squaring with Pieces of Small Boundary and Low Borel Complexity
嗨老伙计,新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(。・∀・)ノ゙