大家好我是渡鸦，今天和大家聊一聊下面这张图片的来龙去脉。（图片来源[1]，点开图片看大图）
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ
集合·几何：一份化圆为方指南
水贴：茱莉亚集合动图两幅
π节/白色情人节快乐！我是渡鸦，最近没什么时间写新的文，以后可能要不定期地鸽下去了咕咕。今天意外地翻到了自己一年前做过的动图，所以滥竽充数地发一篇看图贴了，希望大家理解。
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ
集合论：无穷乘客消失之谜
大家好我是渡鸦，几天前网友sepia大大分享了这么一个谜题（感谢！）：
一个\(\omega_1\)个车站的轨道上，行驶着一辆谜之火车。火车从0号车站出发的时候，车上一个人也没有。之后，火车在1号车站、2号车站……每一站停车的时候，如果车上有人就会有1个人下车，之后有\(\omega\)个新的乘客上车。当火车到达\(\omega_1\)号车站的时候，还有多少人正在车上呢？
这其中\(\omega\)指的是可数无穷，而\(\omega_1\)指的是最小的不可数无穷。如标题所示，这个问题的答案正是：0人。你猜到了吗？
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ
功败垂成的四色定理：被埋没的史话
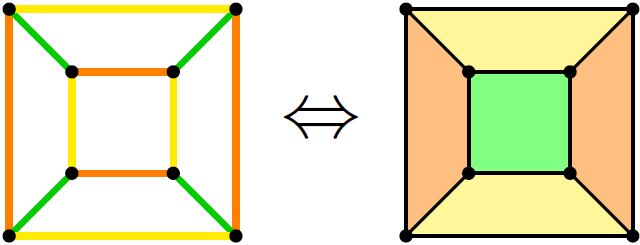
大家好我是渡鸦，两年前我在B站发表了一篇《图论：如何错误地证明四色定理》，今天来聊一聊当时由于篇幅原因被忽略掉的另一个四色定理的“错误证明”吧。
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ
求导证明披萨定理
离散傅里叶变换一则：中点多边形谜题
把一个多边形的各边中点相邻连接得到更小的多边形，不断重复，得到的结果会越来越“圆”吗？答案是不一定。
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ
π的恒等式一则，和灯塔
大家好我是bot鸦，这个博客逐渐变成数学网站，不好意思了
今天用3b1b的灯塔方法简单证明下面这个等式：
\[\frac1{1^3}-\frac1{3^3}+\frac1{5^3}-\frac1{7^3}+\frac1{9^3}\pm\cdots=\frac{\pi^3}{32}\]
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ
生成函数趣题三则
大家好我是渡鸦，好像这周悟理停更了，正好我放假了我更一期。
今天的文章里我来简单介绍一下生成函数的概念，之后会用它解决三道具有一定代表性的例题。
（出于阅读的连贯性考虑，以下是很基础的介绍，可以跳过不看）
生成函数，或者也叫做“母函数”，就是可以包含下某个数列的全部信息的函数的统称。通常说来生成函数都会比它所代表的数列包含一些甚至许多更好用的性质，然后我们就可以利用这些额外的性质来得到一些关于数列本身的结论。
嗨老伙计，新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(｡･∀･)ﾉﾞ