功败垂成的四色定理：被埋没的史话

大家好我是渡鸦，两年前我在B站发表了一篇《图论：如何错误地证明四色定理》，今天来聊一聊当时由于篇幅原因被忽略掉的另一个四色定理的“错误证明”吧。

彼得·泰特（Peter Tait）是一位苏格兰的数学物理学和热动力学家。同上一期所说，在1879年的肯普发表了著名的肯普链证明之后，泰特紧跟着在1880年发表了他自己的证明。

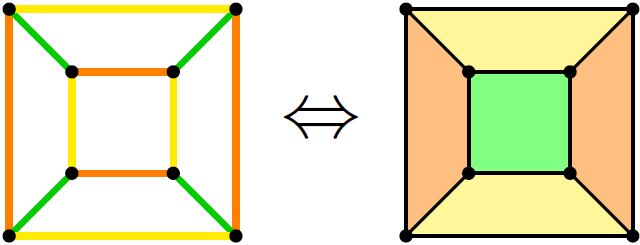
证明的第一步，是意识到给全部平面图染色，等价于给满足每个顶点都连有恰好3条边的全部平面图染色。例如，假如要染色的平面图中的某一个顶点连有4条边，那么以下的局部微扰可以把这样的顶点分裂成两个连有3条边的顶点：

对连更多边的顶点也可以如此操作，这个方法在对偶图意义上就叫做三角剖分。

下一步是先给图的每条边染色。和给图的每个面染色类似，这里的规则是只使用三种颜色，且每个顶点相连的三条边都需要有不同的颜色，例如：

在这样的染色中，考虑删掉被染上某一种特定颜色的所有边。由于图中本来所有顶点都连接三种颜色的边，这样删掉之后得到的新图中每个点都连着恰好2条边，而这样性质的图就只是一个或多个不相交的多边形。例如，从上面的这个图出发就会得到这样的结果：

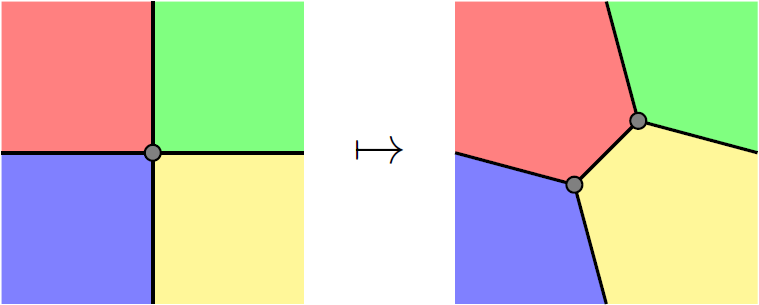
从这三种结果中任意挑出两种，例如前两种，称被它们包围起来的阴影部分为A和B。现在回到原始的图中，每个面都分别有“在A内外”和“在B内外”的总共2×2=4种状态。将这样的状态全部标出之后看起来就是这样的：

仔细看可以发现，任意两个相邻的区域的状态都不一样。这是因为，两个相邻区域之间相隔的边总是青色、粉色或者黄色。如果两个区域相隔青色边，那么由于青色边总是B多边形的边界，它们的B状态就不一样。如果两个区域相隔粉色边，那么由于这是一条A边界，它们的A状态就不一样。如果两个区域相隔黄色边，那么同理它们的A、B状态就都不一样。由于这样的状态正好是四种，所以把字母替换成颜色，就能自动得到图的4-染色：

有了颜色，这里隐藏的另一个对称性就明显许多了：考虑先从面的4-染色着手，构造边的3-染色。那么可以发现，如果一条边相邻的两个面都不是白色，那么这条边就是这两个面的加色。如果一条边相邻的其中一个面是白色，那么这条边就是另外一个面的补色。用更晦涩的术语描述的话，这样的一对边-面染色过程就等价于克莱因4-群上所有非单位元的乘作用。

确实如此，我们马上就可以证明出面的4-染色和边的3-染色其实是等价的。只需要证明的是这样构造出的边3-染色能使得两个同色的边不会出现在同一个顶点上即可。反过来假设存在这样的同色边u和v，那么由于每个顶点只连接了3条边，这两条u和v一定连在同一个面M上。根据染色规则，由于u和v同色，那么在u和v另外一边的剩下两个面也同色，这是不可能的。

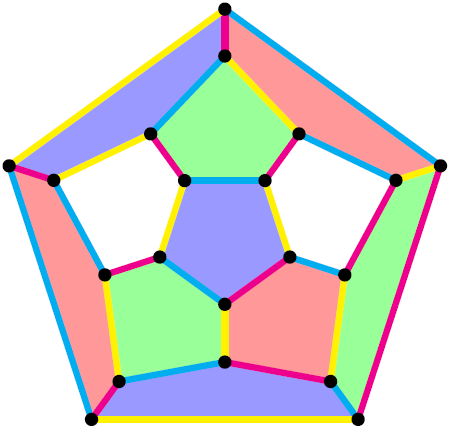
这个四色定理的证明看似完美，但是我们还没说明为什么一定会存在这样的边3-染色。根据我自己的查证，泰特并没有给出染色的逐步过程，也许他是觉得先给出任意的边4-染色或者5-染色、然后再通过肯普交换（见上一期）就可以消掉其中一种或两种颜色吧；由于没有记载下来，他的思路我不得而知。事实上，给任意每个顶点连3条边的平面图构造边的3-染色并不简单，比如我们可以证明出下面的这张图就不存在边3-染色：

图片来源：维基百科

这个图中总共有16个顶点和24条边，因此如果存在3-染色，那么每种颜色都会占满16个顶点，也即每种颜色都包含8条边。但是图中任意画出8条边，总会有其中两条边在某一个顶点处相遇（试试看），因此想要的染色也不存在。

这个图不能构成泰特证明的反例，因为图中正中心的边并没有分隔开两个不同的区域。但是这也说明了，不花一些功夫用到图的更多性质是构造不出满意的染色方案的。上回说到，肯普的证明从1879到1890的11年才被希伍德提出有效质疑。而泰特于肯普后一年1880提出他的证明之后，也过了11年，在肯普被质疑之后的1891年被朱利叶斯·彼得森（Julius Petersen）提出有效质疑。说起彼得森，就不得不提到著名的彼得森图，它除了不是个平面图以外、满足构成泰特的反例的所有性质：

图片来源：维基百科

彼得森图虽以彼得森命名，但是实际在1886的发现者是我们熟悉的肯普先生。自从这个图的性质被彼得森于1898年发表以来，它至今不断充当着诸多图论和组合学里伪命题的反例。

我们说回到泰特。在他的证明被驳回后，他重新着手考虑起一类叫做哈密顿图的图。假设从一个图的其中一个顶点出发，沿着图里的各个边行走。如果可以造访图里的所有顶点各恰好一次，还能在旅途的最后回到开始的定点上，那么这样的图就叫做哈密顿图，走过的路径就叫做哈密顿回路。例如，最开始的边3-染色里，每个阴影多边形的边界都是图的一条哈密顿回路。

那么假设我们有了一个哈密顿图，接下来首先证明图里一定有偶数个顶点。由于我们假设过每个顶点都连有3条边，而每条边连有2个顶点，那么把所有的边都劈成两半，每半分给其中一个顶点，那么图就被分解成了每个顶点连有3/2条边的许多Y字形，因此边的数量和顶点的数量的比也是3:2。所以由于顶点占了比例的其中两份，总顶点数也一定是个偶数。

下一步是找到任意一条哈密顿回路。由于图中总共有偶数个顶点，回路里也一定有偶数个顶点，因此也一定有偶数条边，因为它是一个多边形。用两种颜色交替地给回路的边染色之后，把图的剩下所有边染上第三种颜色，就能得到边的3-染色。这是因为，每个顶点都在哈密顿回路里，所以总会先被染上回路的两种不同颜色，然后再被染上第三种。这样就得到了，所有哈密顿图都满足四色定理。

由于哈密顿图在图论里足够常用，人们发现了许多判断图是不是哈密顿图的根据，例如：
• 所有正多面体都是哈密顿图；
• 有至少5个顶点的平面图，如果去掉任意3个顶点之后仍然是连通的，那么这是一个哈密顿图（Tutte 1956）；
• 有n个顶点的图，如果每条边连接的两个顶点各自所连的边数之和大于等于n，那么这是一个哈密顿图（Ore 1960）；
• 如果一个平面图中有且只有一个面的边数不是3k+2型的整数，那么这不是一个哈密顿图（Grinberg 1968）；
等等。

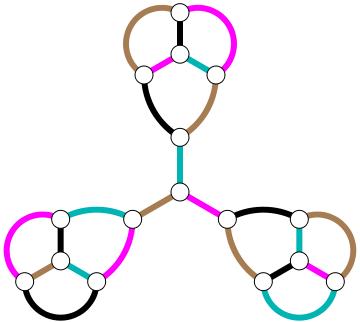
泰特写道，凭一己之力无法证明是不是所有每个顶点连有3条边的平面图都是哈密顿图，也即是不是哈密图的情况涵盖了所有情况。威廉·图特（William Tutte）在1946年找到了反例：

图片来源：维基百科