水贴：茱莉亚集合动图两幅

π节/白色情人节快乐！我是渡鸦，最近没什么时间写新的文，以后可能要不定期地鸽下去了咕咕。今天意外地翻到了自己一年前做过的动图，所以滥竽充数地发一篇看图贴了，希望大家理解。

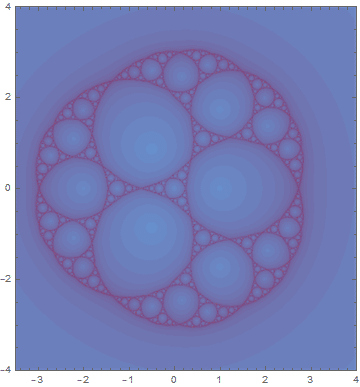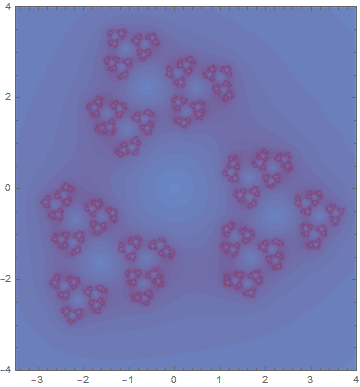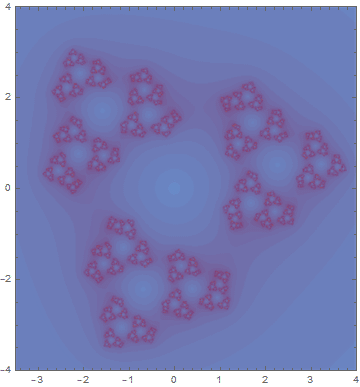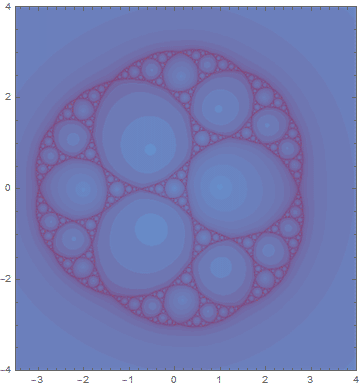
那么首先是这张了。好像上传了之后有点压缩，但是还是能看出来图里的是阿波罗尼斯圆毯和谢尔宾斯基三角之间的转换。不熟悉阿波罗尼斯圆毯的读者朋友可以参考一下一篇Solara大大作过的文章。两者之间的转化是由高阶的茱莉亚分形完成的，最常见的茱莉亚分形就是经常和曼德博集合一起出现的那种了。一年过后的我已经找不到当时做这个图时候调的参数了，依稀地记得好像是把这个分形迭代式的参数在一个三阶傅里叶曲线上循环、然后嵌套进一个正弦波的速度函数吧。总之看得很爽。

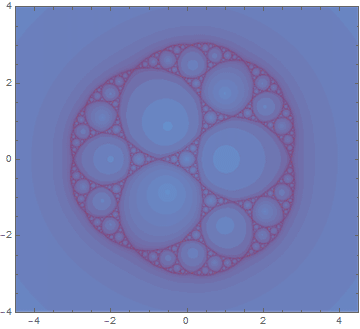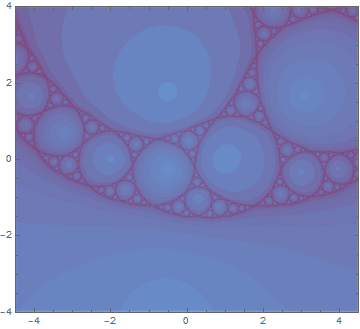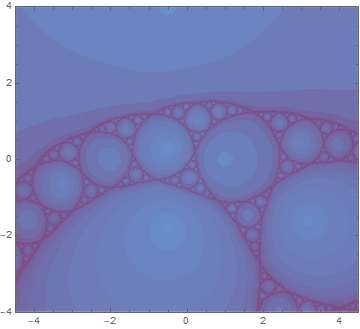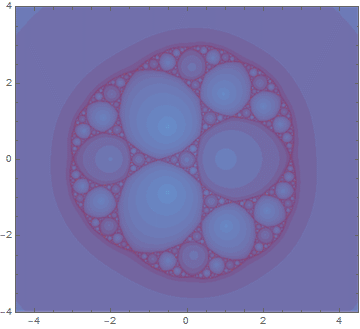
接下来的这一张看起来没有上一张帅了，但是也有比较有意思的地方。因为第一张图做出来阿波罗尼斯圆毯之后就想到，既然阿波罗尼斯圆毯本身在许多射影变换之后的形状不变，那么相对应的茱莉亚集合是不是也有类似的射影对称性呢。往这个方面的研究调查了一下之后发现这一个茱莉亚集合的对称群只是（很小的）保向正四面体旋转群。于是我把其中一个旋转做出来了，仔细就可以发现图里这样旋转三次就恰好转回了一整周。

当然有人可能会问，那么一般的分形图形是不是都有对应的（高阶）茱莉亚集合呢。很遗憾看起来并不是这样，谢尔宾斯基三角形貌似只是一种比较通用的分形形状。类似的谢尔宾斯基方毯有一个开口更多的类似物，但是那个不仔细看的话也看不出很高的相似性（图片也已经找不到了）。再后来的调查过程里我发现，通常的高阶茱莉亚集合的拓扑形状和某一些双曲铺嵌和群论都有些关系，但是当时由于专业性太高就没继续查证下去。现在估计还是看不懂，但是已经没有兴趣了。如果碰巧有对高阶茱莉亚集合有过些了解的读者，欢迎您的赐教。

最后和往常一样，感谢您的阅读。