披萨大家都很熟悉,披萨定理是怎么回事呢?下面就和大家一起了解一下吧。
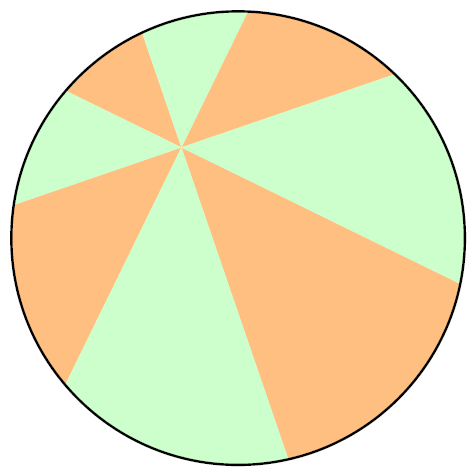
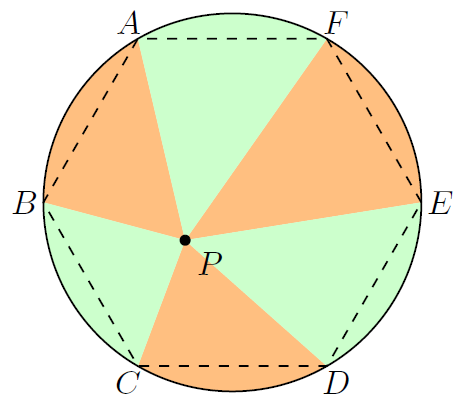
披萨定理是说,在圆内任取一点,从这一点开始把圆分成角度相等的八个部分,得到的如上图中橙色面积和绿色面积相等。这样得到的形状是一个被切成八份的披萨,所以就有了这个很贴切的名字。那么要怎么证明呢?我们先考虑一个独特的引理:
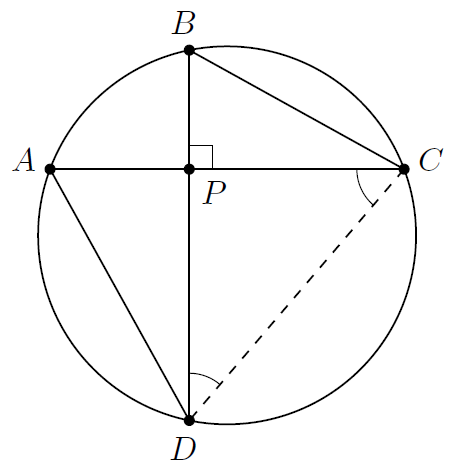
引理1:如图所示,在半径为r的圆内,AC和BD两条弦过P点垂直,那么有
\[AP^2+BP^2+CP^2+DP^2=4r^2\]
证明:左边的式子由于勾股定理,可以写成\(AD^2+BC^2\)。考虑AD和BC两条弦相对的圆周角,在这里等于\(\angle PCD\)和\(\angle PDC\)。因此在同样大小的圆里内接一个相似于\(\triangle PCD\)的直角三角形,两条直角边分别和AD、BC长度相等,斜边是直径,因此有\(AD^2+BC^2=4r^2\)。QED
接下来,求导的方法可以把上面长度的结论转换成面积:
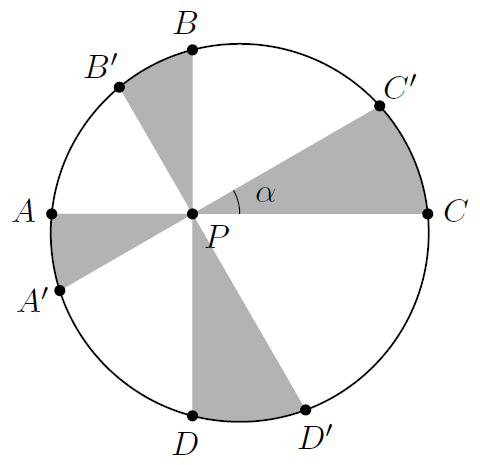
引理2:如图所示,固定半径r的圆,弦\(AC\perp BD\)、\(A’C’\perp B’D’\)汇于点P,那么阴影部分面积仅取决于α。
证明:考虑固定ABCDP五个点,然后把阴影部分面积关于α求微分。这个微分来自于A’B’C’D’绕P点旋转带来的面积变化,它分布在A’P、B’P、C’P、D’P四条线段上。考虑其中的线段A’P,它上面的面积变化可以近似看作一个底边在A’点,斜边在A’P上的等腰三角形,面积等于\(\frac{1}{2}A’P^2d\alpha\)。同理可知总面积的微分就等于
\[\left(A’P^2+B’P^2+C’P^2+D’P^2\right)\frac{d\alpha}{2}=2r^2d\alpha\]
由于引理1,这个微分可以转化成等式右侧的形式,因此可知阴影部分面积就等于\(2r^2\alpha\)了。QED
从这开始,披萨定理的结论就变得呼之欲出了:
披萨定理的证明:由引理2,披萨中的橙色和绿色面积都对应\(\alpha=45^\circ\),因此橙色部分面积等于绿色部分面积。QED
稍加留意就可以发现,这里引理2的结论其实比披萨定理本身还要强一些。例如,稍微更改一下α就可以得到一个三等分的披萨定理:
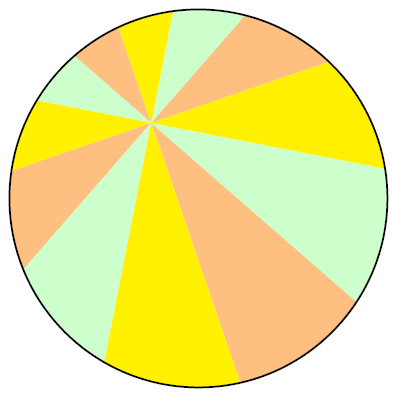
图中的圆形被分成了角度相等的十二份,用和一样的论证可以看出图中橙色、绿色和黄色的面积都是相等的。
不难发现,我们可以继续构造出16份、20份等等的披萨定理。因此下一个问题就是:一般化的披萨定理会对哪些数字成立呢?下面考虑一种不一样的证明思路。

引理3:如图所示,令\(n\ge2\)并把两条平行线称作正2边形,在平面内固定一边长为a的正n边形并任取一点P,那么从P点到n条边作n条垂线,这些垂线的有向长度和恒为定值。
证明:当n=2的时候结论是显然的。接下来考虑P点到边AB的垂线的有向长度h。在\(\triangle PAB\)中,三角形的有向面积就等于\(ah/2\)。因此把这样的三角形面积关于所有垂线求总和,假设所有垂线的有向长总和为H,就会得到正n边形的面积S等于\(aH/2\),也即\(H=2S/a\)。QED
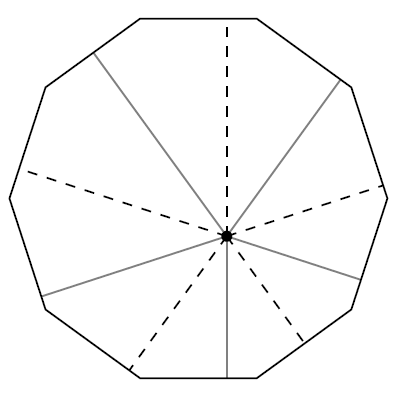
引理4:如图所示,图中灰色线段总长和虚线线段总长相等。更一般地,取\(m,n\ge2\),固定正mn边形与平面内一点。从正mn边形的一条边开始,每数n条边就从该点到最后一条边引一条垂线,从而m条垂线的有向长度总和与m条边的位置无关。
证明:

QED
引理5:如图所示,橙色面积和绿色面积相等。更一般地,当\(m,n\ge2\)时,固定一个圆和圆上均匀分布的mn个点。固定圆内一点P,并以和引理4相似的方式在圆上均匀选取m段圆弧。以其中每一段圆弧和P点相连为边界构造不规则扇形,那么m个扇形的面积总和不取决于圆弧的选择。
证明:这里只解决图例中的情况,一般的情况类似。假设六边形边长为a。从引理4的结论出发,把P点向六边形所有橙色边的有向垂线长总和乘以a/2。由于这个乘积恒定,可以得到在六边形内的橙色有向面积等于六边形内的绿色有向面积(这里有向面积是为了能对P在圆形之内六边形之外的情况也适用)。由于圆形之内、六边形之外的橙色有向面积显然等于绿色有向面积,可以得到图中橙色总面积等于绿色总面积。QED
引理5和披萨定理在形式上相似但不完全相同,下一个引理可以完成二者之间的转化:
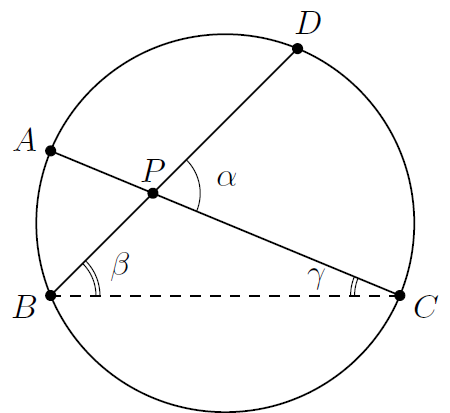
引理6:如图所示,半径为r的固定圆内,弦AC和BD以夹角\(\angle CPD=\alpha\)相交于P。那么弧\(\widehat{AB}\)和弧\(\widehat{CD}\)的长度之和仅取决于α。
证明:令\(\beta=\angle PBC\)以及\(\gamma=\angle PCB\)。由圆周角定理可知\(\widehat{AB}=2r\gamma\)且\(\widehat{CD}=2r\beta\)。在\(\triangle PBC\)中有\(\alpha=\beta+\gamma\),于是得到\(\widehat{AB}+\widehat{CD}=2r\alpha\)。QED
接下来就是最后的证明:

一般披萨定理:令\(m,n\ge2\)。如图所示,在大圆O内取一点P,以P为中心构造角度均匀的2mn条直线,并将圆O分成2mn个不规则扇形。用和之前相似的方式将2mn个扇形间隔均匀地分成n份,每一份含有2m个不规则扇形。那么每一份2m个扇形的面积和恒定。
证明:固定O、P以及2mn条直线的位置,并把橙色总面积和绿色总面积同时对大圆O的半径r求微分。此时,每种颜色的面积的微分来自于这种颜色所占大圆O上的弧长。由引理6,橙色和绿色所占大圆上的弧长总长相等,因此在r变动时,两者的微分也相等。当r缩小至使P位于圆O的边界上时,得到图中的小圆,于是在大圆和小圆之间的环形部分内,橙色和绿色面积相等。
在小圆之内,由圆周角定理得到过P的所有直线交小圆于一个异于P的正mn边形。因此由引理5,小圆内的橙色面积和绿色面积相等。因此大圆之内,橙色和绿色的面积也相等。QED
不难验证,引理2涵盖了所有m=2的情况,且原始的披萨定理满足m=n=2。还存不存在上面的定理也涵盖不到的其他情况呢?我不知道,但是我猜没有了。¯\_(ツ)_/¯
最后再提供一个方形的披萨定理供读者自行思考:

更新:写完正文我发现了一个有意思的地方,引理1→引理2→披萨定理的论证是可以逆过来的,所以由于一般披萨定理成立,可以得到一个一般的引理1:

推论1:在半径为r的圆中取一点P,过P构造间隔角度相等的\(n\ge2\)条直线,顺次交圆于\(A_1,\ldots,A_{2n}\),那么有
\[A_1P^2+A_2P^2+\ldots+A_{2n}P^2=2nr^2\]
嗨老伙计,新鲜的知识不来瞧一瞧吗
这个博客的博客主可爱极啦(。・∀・)ノ゙


沙发,顺带思考题的解答是固定分割线、把正方形外边框向右平移,直到分割线沿正方形一条对角线对称为止